PCB News - Analysis of the method of PCB signal injection on the printed circuit board

The process of transferring high-frequency energy from the coaxial connector to the printed circuit board (PCB) is usually called signal injection, and its characteristics are difficult to describe. The efficiency of energy transfer varies greatly due to different circuit structures. Factors such as PCB material and its thickness and operating frequency range, as well as connector design and its interaction with circuit materials will affect performance. Through the understanding of different signal injection settings and the review of some optimization cases of RF and microwave signal injection methods, the performance can be improved.

Achieving effective signal injection is related to design. Generally, wideband optimization is more challenging than narrowband. Generally, high-frequency injection becomes more difficult as the frequency increases, and it may also have more problems as the thickness of the circuit material increases and the complexity of the circuit structure increases.
Signal injection design and optimization

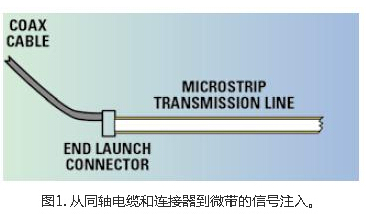
The signal injection from the coaxial cable and connector to the microstrip PCB board is shown in Figure 1. The electromagnetic (EM) field distribution through the coaxial cable and the connector is cylindrical, while the EM field distribution in the PCB is flat or rectangular. From one propagation medium to another, the field distribution will change to adapt to the new environment, resulting in anomalies. The change depends on the type of medium; for example, whether the signal injection is from coaxial cables and connectors to microstrip, grounded coplanar waveguide (GCPW), or strip line. The type of coaxial cable connector also plays an important role.

Optimization involves several variables. It is useful to understand the EM field distribution within the coaxial cable/connector, but the ground loop must also be considered as part of the propagation medium. It is usually helpful to realize a smooth impedance transition from one propagation medium to another. Understanding the capacitive and inductive reactance at impedance discontinuities allows us to understand circuit behavior. If three-dimensional (3D) EM simulation can be performed, the current density distribution can be observed. In addition, it is best to take into account the actual situation related to radiation loss.
Although the ground loop between the signal transmitter connector and the PCB may not seem to be a problem, and the ground loop from the connector to the PCB is very continuous, it is not always the case. There is usually a small surface resistance between the metal of the connector and the PCB. There is also a small difference in the electrical conductivity of the soldering shop that connects the different parts and the metal of these parts. At low RF and microwave frequencies, the impact of these small differences is usually small, but the impact on performance is large at higher frequencies. The actual length of the ground return path will affect the transmission quality that can be achieved with a given connector and PCB combination.

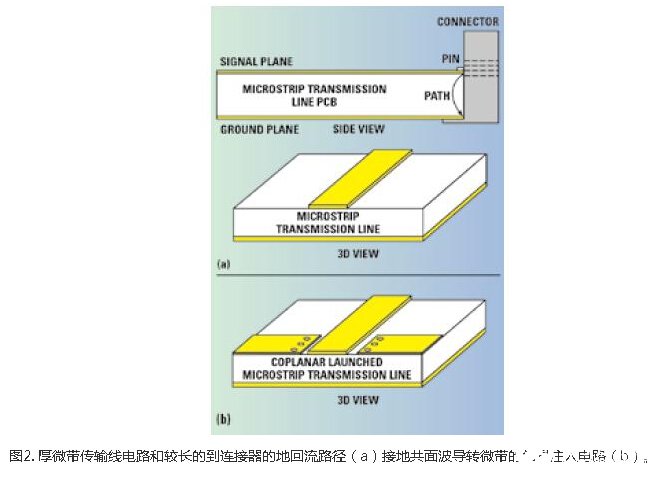
As shown in Figure 2a, when electromagnetic energy is transferred from the connector pins to the signal wires of the microstrip PCB, the ground loop back to the connector housing may be too long for a thick microstrip transmission line. The use of PCB materials with a higher dielectric constant will increase the electrical length of the ground loop, thereby exacerbating the problem. Path extensions can cause frequency-dependent problems, which in turn can cause local phase velocity and capacitance differences. Both are related to the impedance in the transformation area and will affect it, resulting in a difference in return loss. Ideally, the length of the ground loop should be minimized so that there is no impedance anomaly in the signal injection area. Please note that the ground point of the connector shown in Figure 2a only exists at the bottom of the circuit, and this is the worst case. Many RF connectors have ground pins on the same layer as the signal. In this case, the ground pad is also designed on the PCB.
Figure 2b shows the grounded coplanar waveguide to microstrip signal injection circuit. Here, the main body of the circuit is microstrip, but the signal injection area is grounded coplanar waveguide (GCPW). The coplanar emission microstrip is useful because it minimizes ground loops and has other useful characteristics. If you use a connector with ground pins on both sides of the signal wire, the ground pin spacing has a significant impact on performance. It has been shown that this distance affects the frequency response.

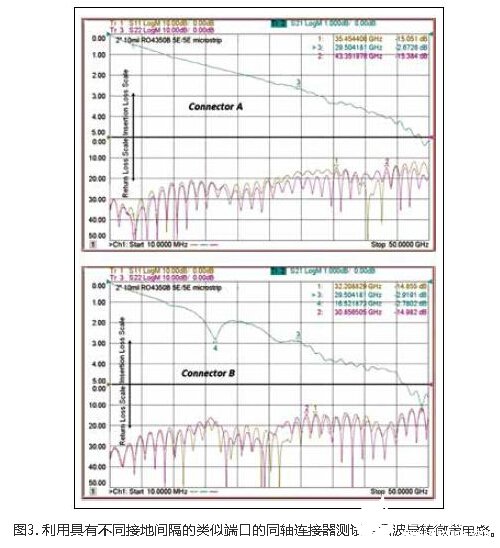
When experimenting with a coplanar waveguide to microstrip microstrip based on Rogers' 10mil-thick RO4350B laminate, a connector with a different grounding distance between the coplanar waveguide port and other parts was used (see Figure 3). The ground separation of connector A is approximately 0.030", and the ground separation of connector B is 0.064". In both cases, the connector transmits to the same circuit.

The x-axis represents frequency, 5 GHz per division. When the microwave frequency is lower (< 5 GHz), the performance is equivalent, but when the frequency is higher than 15 GHz, the performance of the circuit with a larger ground separation becomes worse. The connectors are similar, although the pin diameters of the two models are slightly different, the pin diameter of connector B is larger and is designed for thicker PCB materials. This may also cause performance differences.
A simple and effective signal injection optimization method is to minimize the impedance mismatch in the signal transmitting area. The increase in the impedance curve is basically due to the increase in inductance, while the decrease in the impedance curve is due to the increase in capacitance. For the thick microstrip transmission line shown in Figure 2a (assuming that the dielectric constant of the PCB material is low, about 3.6), the wire is wider-much wider than the inner conductor of the connector. Due to the large difference in the size of the circuit wire and the connector wire, a strong capacitive mutation occurs during the transition. It is usually possible to reduce the capacitive mutation by gradually tapering the circuit wire to reduce the size gap formed at the place where it is connected to the pin of the coaxial connector. Narrowing the PCB wire will increase its inductance (or decrease its capacitance, so as to offset the capacitive mutation in the impedance curve.
The impact on different frequencies must be considered. Longer gradation lines will be more sensitive to low-frequency production. For example, if the return loss is poor at low frequencies and there is a capacitive impedance spike at the same time, it is more appropriate to use a longer gradient line. Conversely, a shorter gradient line has a greater effect on high frequencies.

For coplanar structures, the capacitance will increase when adjacent ground planes are close. Usually, the inductive capacitance of the signal injection area is adjusted in the corresponding frequency band by adjusting the distance between the gradual signal line and the adjacent ground plane. In some cases, the adjacent ground pads of the coplanar waveguide are wider on a section of the tapered line to adjust the lower frequency band. Then, the pitch becomes narrower in the wider part of the gradation line, and the length of the narrower part is not long to affect the higher frequency band. Generally speaking, the narrowing of the wire gradient will increase the sensitivity. The length of the gradient line affects the frequency response. Changing the adjacent ground pads of the coplanar waveguide can change the capacitance. The pad spacing can change the frequency response, which plays a major role in the change of the capacitance.
Instance

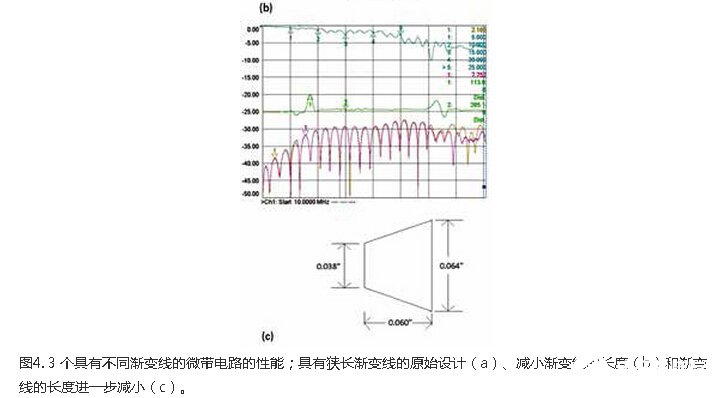
Figure 4 provides a simple example. Figure 4a is a thick microstrip transmission line with long and narrow tapered lines. The gradient line is 0.018" (0.46 mm) wide at the edge of the board, 0.110" (2.794 mm) long, and finally becomes a 50 Ω line width 0.064" (1.626 mm) wide. In Figures 4b and 4c, the length of the gradient line Shortened. The field crimpable terminal connector is selected and is not soldered, so the same inner conductor is used in each case. The microstrip transmission line is 2" (50.8 mm) long and is processed in a 30mil (0.76 mm) thick RO4350B? Microwave circuit On the laminate, the dielectric constant is 3.66. In Figure 4a, the blue curve represents the insertion loss (S21), which fluctuates a lot. In contrast, S21 in Figure 4c has the least amount of fluctuations. These curves show that the shorter the gradient line, the higher the performance.

Perhaps the most illustrative curve in Figure 4 shows the impedance of the cable, connector, and circuit (green curve). The large forward wave peak in Figure 4a represents the connector port 1 connected to the coaxial cable, and the other peak on the curve represents the connector at the other end of the circuit. The fluctuation on the impedance curve is reduced due to the shortening of the gradual change line. The improvement of impedance matching is because the gradation line in the signal injection area becomes wider and narrower; the wider gradation line reduces the inductance.
We can learn more about the circuit size of the injection area from an excellent signal injection design 2. This circuit also uses the same board and the same thickness. A coplanar waveguide to microstrip circuit, through the use of the experience of Figure 4, produced a better effect than Figure 4. The most obvious improvement is to eliminate the inductive peaks in the impedance curve. In fact, this is caused by some inductive peaks and capacitive valleys. Use the correct gradient line to minimize the inductive peak, and use the coplanar ground pad coupling in the injection area to increase the inductance. The insertion loss curve of Figure 5 is smoother than that of Figure 4c, and the return loss curve is also improved. For microstrip circuits using PCB materials with higher dielectric constants or different thicknesses, or microstrip circuits using different types of connectors, the results of the example shown in Figure 4 are different.
Signal injection is a very complex problem, affected by many different factors. This example and these guidelines are designed to help designers understand the basic principles.